Volume Of A Sphere With A Radius Of 3

The unit of volume of a sphere is given as the 3. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere. There are two types of spheres, solid sphere, and hollow sphere.

The volume of both types of spheres is different. We will learn in the following sections about their volumes. A sphere is the shape of a basketball, like a three-dimensional circle. Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below.

In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches. A sphere is a 3-dimensional round object. The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. The volume of sphere is the capacity it has. It is the space occupied by the sphere.

The volume of sphere is measured in cubic units, such as m3, cm3, in3, etc. The shape of the sphere is round and three-dimensional. It has three axes as x-axis, y-axis and z-axis which defines its shape. All the things like football and basketball are examples of the sphere which have volume.

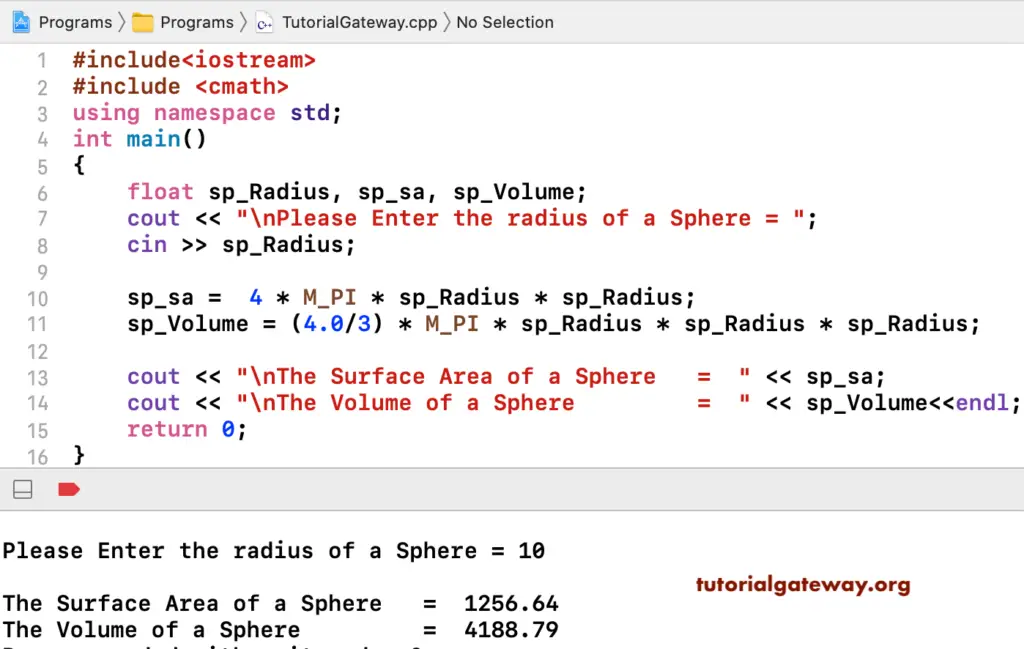
Note- In order to solve this question, we must know the formula of volume of sphere i.e. $\dfrac\pi $. Along with that formula, we must know all the formulas of a sphere like total surface area i.e. $4\pi $ to solve similar kinds of problems. This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C.

It will also give the answers for volume, surface area and circumference in terms of PI π. A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point . In this example you need to calculate the volume of a very long, thin cylinder, that forms the inside of the pipe. The area of one end can be calculated using the formula for the area of a circle πr2. The diameter is 2cm, so the radius is 1cm.

The area is therefore π × 12, which is 3.14cm2. A glass dome for a lighting fixture is in the shape of a hemisphere. The circumference of the great circle of the hemisphere is 12π inches.

Which statements about the hemisphere are true? The total surface area is 108π square inches. The total surface area is 144π square inches. The total surface area is 432π square inches. The total surface area is 36π square inches.

Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you. It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. A sphere is a round shape solid object in three-dimensional space.

It can be defined as the set of points that are all at the same distance from a given point . The perfect example of the sphere is the globe and ball. The following figure shows a sphere shape whose radius is r, and the diameter is d. The baseball is not regulation size. If the baseball has a surface area of 9π, then I can set that equal to the formula 4πr2 and solve for r. The radius is 3/2 inches, so I double that to find the diameter.

The diameter of the ball is 3 inches, which is greater than the allowed range of diameters. A sphere is a three-dimensional solid with no face, no edge, no base and no vertex. It is a round body with all points on its surface equidistant from the center. The volume of a sphere is measured in cubic units.

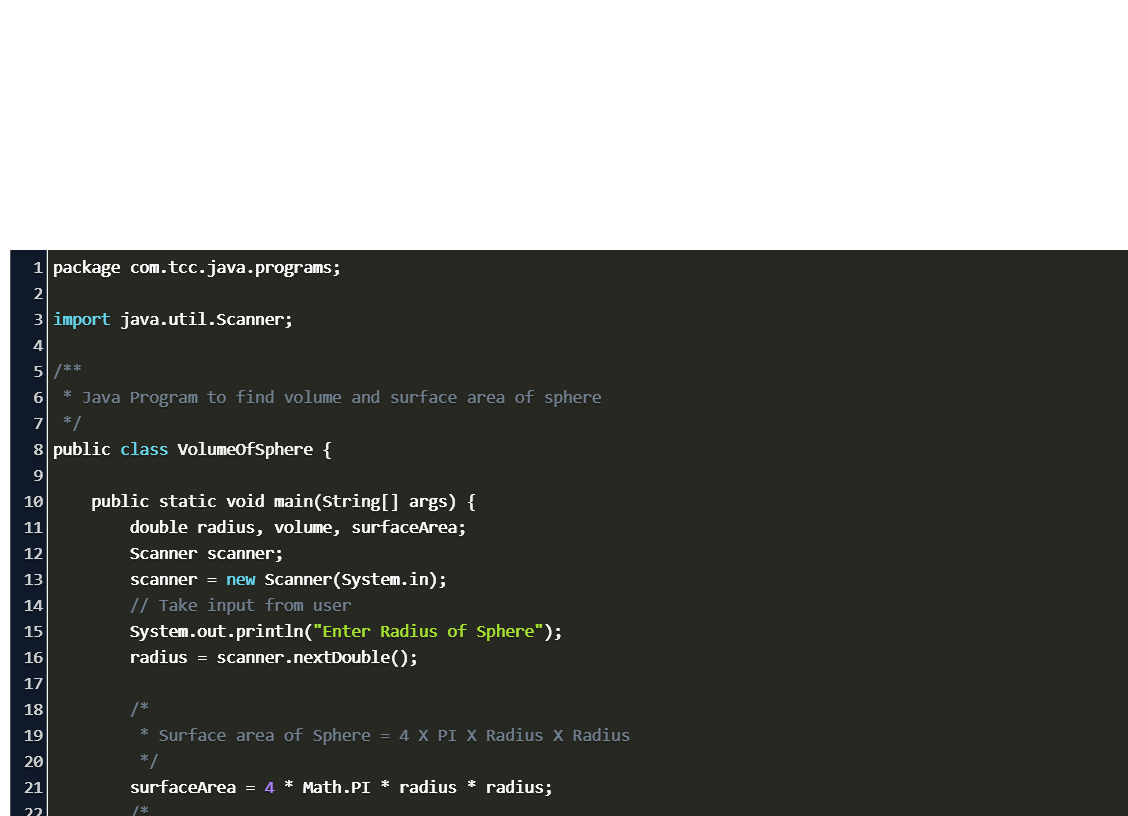
A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center. Given radius of sphere, calculate the volume and surface area of sphere.

The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. There is another special formula for finding the volume of a sphere. The volume is how much space takes up the inside of a sphere. The answer to a volume question is always in cubic units. This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's".

The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious. So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind. If you want to help here I think you should pay attention to new questions that don't yet have answers. The volume of a sphere is the measurement of the space it can occupy. A sphere is a three-dimensional shape that has no edges or vertices.

In this short lesson, we will learn to find the volume of a sphere, deduce the formula of volume of a sphere and learn to apply the formulas as well. Once you understand this chapter you will learn to solve problems on the volume of the sphere. A regulation baseball must have a diameter between 2.87 and 2.94 inches. The surface area of a particular baseball is 9π square inches. Is the baseball within the range of regulation size?

This distance r is the radius of the sphere, and the given point is the center of the sphere. For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere.

A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere.

A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere. All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent.

The formula for the volume of a sphere is 4/3 times pi times the radius cubed. Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. The pi in the formula is the constant that we use when finding the circumference of a circle, and the radius, as you might remember, is half the length of the diameter. The last thing is that the radius is cubed.

This relates to the fact that in the end we are solving for volume, which has three dimensions. Now the question becomes calculating the volume of the bicylinder . It is also very difficult, so add a cube packing the bicylinder . Now when the plane intersects the cube, it forms another larger square. The extra area in the large square , is the same as 4 small squares . Moving through the whole bicylinder generates a total of 8 pyramids.

Let us take an example to learn how to calculate the volume of sphere using its formula. The volume of sphere formula can be given for a solid as well as the hollow sphere. The volume of a sphere is the amount of space occupied by it. For a hollow sphere like a football, the volume can be viewed as the number of cubic units required to fill up the sphere. This concept can be of significance in geometry, to find the volume & surface area of sphere and its parts.

Real life problems on volume & surface area of sphere are very common, so this concept can be of great importance of solving problems. It is a straightforward question, but the visual does not make it clear that the inner sphere is empty especially when the text of the question doesn't make it apparent. I was stuck on it for a while on GMATPrepExam, then assumed that the question is asking for the difference in volume adjusted weight. It is surprising because in PS questions, the stem is generally very clear and without any ambiguity. For example, even in the same question - formula of a sphere is provided. Most of the times, PS questions don't mind giving redundant information through text that is already there in the pic.

A globe of Earth is in the shape of a sphere with radius 14[/latex] centimeters. Round the answer to the nearest hundredth. The volume of a 3 -dimensional solid is the amount of space it occupies.

Be sure that all of the measurements are in the same unit before computing the volume. A surface has no volume, hence, we prefer to refer to it as a ball. Try the free Mathway calculator and problem solver below to practice various math topics.

Try the given examples, or type in your own problem and check your answer with the step-by-step explanations. The volume of a hemisphere is equal to two-thirds of the product of pi and the cube of the radius. The following figure gives the formula for the volume of sphere. Scroll down the page for examples and solutions. The sphere is an extended version of a circle. Or it will be right to say a 3D version of a circle.

In geometry, a sphere is a 3-dimensional round solid figure in which every point on its surface is equidistant from its center. Bunuel For the volume of the sphere why are we taking "outer radius 5r" and "inner radius 2r" for the volume of the empty space? I can't identify it from the pic which one is the inner or outer radius, which one is solid sphere and spherical shell. The volume of a sphere is four thirds pi times the radius cubed.

So far we've calculated the volume of cubes, rectangular tanks, and cylinders. Using that information, how do you think we would calculate the volume of a sphere? What variables do you think you would use? Take a few moments to think about it before we go through the explanation below. 7Given a solid sphere of radius R, remove a cylinder whose central axis goes through the center of the sphere.

Browse other questions tagged geometry volume solid-geometry spheres or ask your own question. The formula for measuring the volume of a sphere is (4/3)πr3. We can simply measure the volume of any spherical shell by substituting the values of the parameters like radius and diameter in the volume formula. Our radius of a sphere calculator is a perfect tool that can estimate every parameter of a sphere from just one another quantity. However, it is mainly designed to support the computation of sphere radius. Try this calculator now by entering one of the chosen parameters into the appropriate field or read on and learn how to find the radius of a sphere.

In the following text, we have also presented four different radius of a sphere formulas. The volume V of a sphere is four-thirds times pi times the radius cubed. Notice that one thing we can easily find is the area of a single horizontal slice of the ball. This is the shaded disk at the top of the diagram, which is drawn at height z.

The disk has a radius of x, which we'll need to find the area of the disk. To find x, we can form a right triangle with sides z and x, and hypotenuse r. The points have equidistant from the center. In this section, we will learn the volume formula, and also learn how to find the volume of a sphere.